The angle between $\mathbf{A} = \mathbf{\hat{i}} + \mathbf{\hat{j}}$ and $\mathbf{B} = \mathbf{\hat{i}} - \mathbf{\hat{j}}$ is
Which one of the following statements is true?
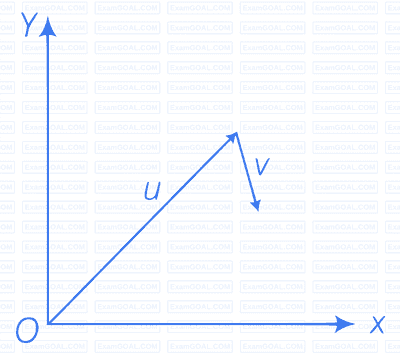
Figure shows the orientation of two vectors u and v in the xy-plane.
If $\mathbf{u} = a\hat{i} + b\hat{j}$ and $\mathbf{v} = p\hat{i} + q\hat{j}$
Which of the following is correct?
The component of a vector r along X-axis will have maximum value if
The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be
Consider the quantities, pressure, power, energy, impulse, gravitational potential, electrical charge, temperature, area. Out of these, the only vector quantities are
In a two dimensional motion, instantaneous speed $v_0$ is a positive constant. Then, which of the following are necessarily true?
In a two dimensional motion, instantaneous speed $v_0$ is a positive constant. Then, which of the following are necessarily true?
Three vectors A, B and C add up to zero. Find which is false.
It is found that |A + B| = |A|. This necessarily implies.
Two particles are projected in air with speed $v_0$ at angles $\theta_1$ and $\theta_2$ (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices.
A particle slides down a frictionless parabolic $(y + x^2)$ track $A – B – C$ starting from rest at point A (figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then

Following are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one(s).
For a particle performing uniform circular motion, choose the correct statement(s) from the following.
For two vectors A and B, |A + B| = |A − B| is always true when

A cyclist starts from centre O of a circular park of radius 1 km and moves along the path OPRQO as shown in figure. If he maintains constant speed of $10 \, \text{ms}^{-1}$, what is his acceleration at point R in magnitude and direction?
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure where x and y indicate horizontal and vertical directions, respectively. Shown in the diagram, direction of velocity and acceleration at points A, B and C.

A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
(a) greatest speed
(b) smallest speed
(c) greatest acceleration
Explain.
A football is kicked into the air vertically upwards. What is its (a) acceleration and (b) velocity at the highest point?
A, B and C are three non-collinear, non co-planar vectors. What can you say about direction of $A \times (B \times C)$?
A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
A boy throws a ball in air at 60° to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of (18 km/h). Give explanation to support your diagram.
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
(a) Earth can be thought of as a sphere of radius 6400 km. Any object (or a person) is performing circular motion around the axis of the earth due to the earth rotation (period 1 day). What is acceleration of object on the surface of the earth (at equator) towards its centre? What is it at latitude 0°? How does these accelerations compare with $g = 9.8 \text{ m/s}^2$?
(b) Earth also moves in circular orbit around the sun once every year with an orbital radius of $1.5 \times 10^{11}$ m. What is the acceleration of the earth (or any object on the surface of the earth) towards the centre of the sun? How does this acceleration compare with $g = 9.8 \text{ m/s}^2$?
Given below in Column I are the relations between vectors a, b and c and in Column II are the orientations of a, b and c in the XY-plane. Match the relation in Column I to correct orientations in Column II.
| Column I | Column II |
|---|---|
| (a) $ a + b = c $ | (i)  |
| (b) $ a - c = b $ | (ii) |
| (c) $ b - a = c $ | (iii)  |
| (d) $ a + b + c = 0 $ | (iv)  |
If $|A|=2$ and $|B|=4$, then match the relation in Column I with the angle $\theta$ between $A$ and $B$ in Column II.
| Column I | Column II |
|---|---|
| (a) $\mathbf{A \cdot B} = 0$ | (i) $\theta = 0^\circ$ |
| (b) $\mathbf{A \cdot B} = +8$ | (ii) $\theta = 90^\circ$ |
| (c) $\mathbf{A \cdot B} = 4$ | (iii) $\theta = 180^\circ$ |
| (d) $\mathbf{A \cdot B} = -8$ | (iv) $\theta = 60^\circ$ |
If $|A|=2$ and $|B|=4$, then match the relations in Column I with the angle $\theta$ between $A$ and $B$ in Column II
| Column I | Column II |
|---|---|
| (a) $\vert \mathbf{A \times B} \vert = 0$ | (i) $\theta = 30^\circ$ |
| (b) $\vert \mathbf{A \times B} \vert = 8$ | (ii) $\theta = 45^\circ$ |
| (c) $\vert \mathbf{A \times B} \vert = 4$ | (iii) $\theta = 90^\circ$ |
| (d) $\vert \mathbf{A \times B} \vert = 4\sqrt{2}$ | (iv) $\theta = 0^\circ$ |
A hill is 500 m high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of 125 m/s over the hill. The canon is located at a distance of 800 m from the foot of the hill and can be moved on the ground at a speed of 2 m/s; so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach on the ground across the hill? Take, $g = 10 \text{ m} / \text{s}^2$.
A gun can fire shells with maximum speed $v_0$ and the maximum horizontal range that can be achieved is $R = \dfrac{v_0^2}{g}$ If a target farther away by distance $\Delta x$ (beyond $R$) has to be hit with the same gun, show that it could be achieved by raising the gun to a height at least
$h = \Delta x \left[1 + \dfrac{\Delta x}{R}\right]$

A particle is projected in air at an angle $\beta$ to a surface which itself is inclined at an angle $\alpha$ to the horizontal (figure).
(a) Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
(b) Time of flight.
A particle falling vertically from a height hits a plane surface inclined to horizontal at an angle $\theta$ with speed $v_0$ and rebounds elastically. Find the distance along the plane where it will hit second time.

A girl riding a bicycle with a speed of 5 m/s towards north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground-based observer?
A river is flowing due east with a speed 3 m/s. A swimmer can swim in still water at a speed of 4 m/s (figure).
(a) If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction)?
(b) If he wants to start from point A on south bank and reach opposite point B on north bank,
(i) which direction should he swim?
(ii) what will be his resultant speed?
(c) From two different cases as mentioned in (a) and (b) above, in which case will he reach opposite bank in shorter time?

(a) the effective angle to the horizontal at which the ball is projected inair as seen by a spectator.
(b) what will be time of flight?
(c) what is the distance (horizontal range) from the point of projection at which the ball will land?
(d) find $\theta$ at which he should throw the ball that would maximise the horizontal range as found in (iii).
(e) how does $\theta$ for maximum range change if $u > u_0, u = u_0, u < v_0$?
(f) how does $\theta$ in (v) compare with that for $u = 0 \ (i.e., 45^\circ)$?
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates $ \mathbf{A} = A_x \hat{i} + A_y \hat{j} $, where $ \hat{i} $ and $ \hat{j} $ are unit vector along x and y-directions, respectively and $ A_x $ and $ A_y $ are corresponding components of $ \mathbf{A} $. Motion can also be studied by expressing vectors in circular polar coordinates as $ \mathbf{A} = A_r \hat{r} + A_\theta \hat{\theta} $, where $ \hat{r} = \frac{\mathbf{r}}{r} = \cos{\theta} \hat{i} + \sin{\theta} \hat{j} $ and $ \hat{\theta} = -\sin{\theta} \hat{i} + \cos{\theta} \hat{j} $ are unit vectors along direction in which r and $ \theta $ are increasing.
(a) Express $ \hat{i} $ and $ \hat{j} $ in terms of $ \hat{r} $ and $ \hat{\theta} $.
(b) Show that both $ \hat{r} $ and $ \hat{\theta} $ are unit vectors and are perpendicular to each other.
(c) Show that $ \frac{d}{dt} ( \hat{r}) = \omega \hat{\theta} $, where $ \omega = \frac{d\theta}{dt} $ and $ \frac{d}{dt} ( \hat{\theta}) = - \omega \hat{r} $.
(d) For a particle moving along a spiral given by $ r = a \theta \hat{r} $, where $ a = 1 $ (unit), find dimensions of a.
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
A man wants to reach from A to the opposite corner of the square C. The sides of the square are 100 m. A central square of 50m × 50m is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square, he can walk only at a speed v m/s (v < 1). What is the smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?
