If $|A|=2$ and $|B|=4$, then match the relation in Column I with the angle $\theta$ between $A$ and $B$ in Column II.
| Column I | Column II |
|---|---|
| (a) $\mathbf{A \cdot B} = 0$ | (i) $\theta = 0^\circ$ |
| (b) $\mathbf{A \cdot B} = +8$ | (ii) $\theta = 90^\circ$ |
| (c) $\mathbf{A \cdot B} = 4$ | (iii) $\theta = 180^\circ$ |
| (d) $\mathbf{A \cdot B} = -8$ | (iv) $\theta = 60^\circ$ |
Given $|A| = 2$ and $|B| = 4$:
(a) $A \cdot B = AB \cos \theta = 0$
$\Rightarrow 2 \times 4 \cos \theta = 0$
$\Rightarrow \cos \theta = 0 = \cos 90^\circ$
$\Rightarrow \theta = 90^\circ$
Thus, option (a) matches with option (ii).
(b) $A \cdot B = AB \cos \theta = 8$
$\Rightarrow 2 \times 4 \cos \theta = 8$
$\Rightarrow \cos \theta = 1 = \cos 0^\circ$
$\Rightarrow \theta = 0^\circ$
Thus, option (b) matches with option (i).
(c) $A \cdot B = AB \cos \theta = 4$
$\Rightarrow 2 \times 4 \cos \theta = 4$
$\Rightarrow \cos \theta = \frac{1}{2} = \cos 60^\circ$
$\Rightarrow \theta = 60^\circ$
Thus, option (c) matches with option (iv).
(d) $A \cdot B = AB \cos \theta = -8$
$\Rightarrow 2 \times 4 \cos \theta = -8$
$\Rightarrow \cos \theta = -1 = \cos 180^\circ$
$\Rightarrow \theta = 180^\circ$
Thus, option (d) matches with option (iii).
If $|A|=2$ and $|B|=4$, then match the relations in Column I with the angle $\theta$ between $A$ and $B$ in Column II
| Column I | Column II |
|---|---|
| (a) $\vert \mathbf{A \times B} \vert = 0$ | (i) $\theta = 30^\circ$ |
| (b) $\vert \mathbf{A \times B} \vert = 8$ | (ii) $\theta = 45^\circ$ |
| (c) $\vert \mathbf{A \times B} \vert = 4$ | (iii) $\theta = 90^\circ$ |
| (d) $\vert \mathbf{A \times B} \vert = 4\sqrt{2}$ | (iv) $\theta = 0^\circ$ |
Given $|A| = 2$ and $|B| = 4$
(a) $|A \times B| = AB \sin \theta = 0$
$ \Rightarrow 2 \times 4 \sin \theta = 0 $
$ \Rightarrow \sin \theta = 0 = \sin 0^\circ $
$ \Rightarrow \theta = 0^\circ $
$ \therefore \text{Option (a) matches with option (iv).} $
(b) $|A \times B| = AB \sin \theta = 8$
$ \Rightarrow 2 \times 4 \sin \theta = 8 $
$ \Rightarrow \sin \theta = 1 = \sin 90^\circ $
$ \Rightarrow \theta = 90^\circ $
$ \therefore \text{Option (b) matches with option (iii).} $
(c) $|A \times B| = AB \sin \theta = 4$
$ \Rightarrow 2 \times 4 \sin \theta = 4 $
$ \Rightarrow \sin \theta = \frac{1}{2} = \sin 30^\circ $
$ \Rightarrow \theta = 30^\circ $
$ \therefore \text{Option (c) matches with option (i).} $
(d) $|A \times B| = AB \sin \theta = 4 \sqrt{2}$
$ \Rightarrow 2 \times 4 \sin \theta = 4 \sqrt{2} $
$ \Rightarrow \sin \theta = \frac{1}{\sqrt{2}} = \sin 45^\circ $
$ \Rightarrow \theta = 45^\circ $
$ \therefore \text{Option (d) matches with option (ii).} $
A hill is 500 m high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of 125 m/s over the hill. The canon is located at a distance of 800 m from the foot of the hill and can be moved on the ground at a speed of 2 m/s; so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach on the ground across the hill? Take, $g = 10 \text{ m} / \text{s}^2$.
Given, speed of packets = 125 m/s
Height of the hill = 500 m.
To cross the hill, the vertical component of the velocity should be sufficient to cross such height.
$u_y \geq \sqrt{2gh}$
$\geq \sqrt{2 \times 10 \times 500}$
$\geq 100 \text{m/s}$
But
$u^2 = u_x^2 + u_y^2$
$\therefore$ Horizontal component of initial velocity,
$u_x = \sqrt{u^2 - u_y^2} = \sqrt{(125)^2 - (100)^2} = 75 \text{ m/s}$
Time taken to reach the top of the hill,
$t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 500}{10}} = 10 \text{ s}$
Time taken to reach the ground from the top of the hill $t' = t = 10 \text{ s}$. Horizontal distance travelled in 10 s
$x = u_x \times t = 75 \times 10 = 750 \text{ m}$
$\therefore$ Distance through which canon has to be moved = 800 – 750 = 50 m
Speed with which canon can move = 2 m/s
$\therefore$ Time taken by canon = $\frac{50}{2}$ $\Rightarrow$ $t'' = 25 \text{ s}$
$\therefore$ Total time taken by a packet to reach on the ground = $t'' + t + t' = 25 + 10 + 10 = 45$ s
A gun can fire shells with maximum speed $v_0$ and the maximum horizontal range that can be achieved is $R = \dfrac{v_0^2}{g}$ If a target farther away by distance $\Delta x$ (beyond $R$) has to be hit with the same gun, show that it could be achieved by raising the gun to a height at least
$h = \Delta x \left[1 + \dfrac{\Delta x}{R}\right]$

This problem can be approached in two different ways
(i) Refer to the diagram, target $T$ is at horizontal distance $x = R + \Delta x$ and between point of projection $y = -h$.
(ii) From point $P$ in the diagram projection at speed $v_0$ at an angle $\theta$ below horizontal with height $h$ and horizontal range $\Delta xA$)
Applying method (i)
Maximum horizontal range
$$R = \frac{{v_0^2}}{g}, \text{ for } \theta = 45^\circ\quad \text{...(i)}$$
Let the gun be raised through a height h from the ground so that it can hit the target. Let vertically downward direction be taken as positive.
Horizontal component of initial velocity = v0 cosθ
Vertical component of initial velocity = −v0 sinθ
Taking motion in vertical direction,
$ h = (-v_0 \sin\theta) \, t + \frac{1}{2} \, g \, t^2 $ ... (ii)
Taking motion in horizontal direction
$(R + Δx) = v_0 \cos\theta \times t $
$\Rightarrow$ $ t = \frac{(R + Δx)}{v_0 \cos\theta} $ ... (iii)
Substituting value of t in Eq. (ii), we get
$ \begin{align*} h &= \left(-v_0 \sin\theta \right) \times \left( \frac{R + Δx}{v_0 \cos\theta} \right) + \frac{1}{2} \, g \, \left( \frac{R + Δx}{v_0 \cos\theta} \right)^2 \\ h &= - (R + Δx) \tan\theta + \frac{1}{2} \, g \, \frac{(R + Δx)^2}{v_0^2 \cos^2\theta} \end{align*} $
$\begin{align*} &\text{As angle of projection is } \theta = 45^\circ, \text{ therefore} \\\\ & h = -(R + \Delta x) + \tan 45^\circ + \frac{1}{2} \frac{g\ (R + \Delta x)^2}{v_0^2 \cos^2 45^\circ} \\\\ & h = -(R + \Delta x) \times 1 + \frac{1}{2} \frac{g \ (R + \Delta x)^2}{v_0^2 (1/2)} \quad \left(\because \tan 45^\circ = 1 \text{ and } \cos 45^\circ = \frac{1}{\sqrt{2}}\right) \\\\ & h = -(R + \Delta x) + \frac{(R + \Delta x)^2}{R} \quad \text{[Using Eq. (i), } R = \frac{v_0^2}{g}] \\\\ & = -(R + \Delta x) + \frac{1}{R}(R^2 + \Delta x^2 + 2R\Delta x) \\\\ & = -R - \Delta x + \left( R + \frac{\Delta x^2}{R} + 2\Delta x \right) \\\\ & = \Delta x + \frac{\Delta x^2}{R} \\\\ & h = \Delta x \left( 1 + \frac{\Delta x}{R} \right) \\\\ & \text{Hence proved.} \end{align*}$
Note We should not confuse with the positive direction of motion. May be vertically upward direction or vertically downward direction is taken as positive according to convenience.
A particle is projected in air at an angle $\beta$ to a surface which itself is inclined at an angle $\alpha$ to the horizontal (figure).
(a) Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
(b) Time of flight.
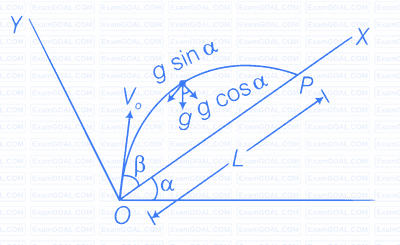
Consider the adjacent diagram.
Mutually perpendicular x and y-axes are shown in the diagram.
Particle is projected from the point O.
Let time taken in reaching from point O to point P is T.
(b) Considering motion along vertical upward direction perpendicular to OX.
For the journey O to P.
$ \begin{align*} & y = 0, \ u_y = v_0 \sin \beta, \ a_y = -g \cos \alpha, \ t = T \\ & \text{Applying equation,} \\ & y = u_y t + \frac{1}{2} a_y t^2 \\ & \implies 0 = v_0 \sin \beta T + \frac{1}{2}(-g \cos \alpha) T^2 \end{align*} $
$\Rightarrow \ T \left[ v_0 \sin \beta - \frac{g \cos \alpha}{2} T \right] = 0 $
$\Rightarrow \quad T = 0, \ T = \frac{2\ v_0 \sin \beta}{g \cos \alpha} $
As $ T = 0 $, corresponding to point $ O $
Hence, $T = \text{Time of flight} = \frac{2\ v_0 \sin \beta}{g \cos \alpha} $
(a)$\text{ Considering motion along } OX.$
$ x = L, u_x = v_0 \cos \beta, a_x = -g \sin \alpha $
$ t = T = \frac{2\ v_0 \sin \beta}{g \cos \alpha} $
$ x = u_x t + \frac{1}{2} a_x t^2 $
$\begin{align*} \implies & \quad L = v_0 \cos \beta \ T + \frac{1}{2} (-g \sin \alpha) \ T^2 \\\\ \implies & \quad L = v_0 \cos \beta \ T - \frac{1}{2} g \sin \alpha \ T^2 \\\\ & \quad = T \left[v_0 \cos \beta - \frac{1}{2} g \sin \alpha \ T \right] \\\\ & \quad = T \left[ v_0 \cos \beta - \frac{1}{2} g \sin \alpha \times \frac{2 v_0 \sin \beta}{g \cos \alpha} \right] \\\\ & \quad = \frac{2 \ v_0 \sin \beta}{g \cos \alpha} \left[ v_0 \cos \beta - \frac{v_0 \sin \alpha \sin \beta}{\cos \alpha} \right] \\\\ & \quad = \frac{2 \ v_0^2 \sin \beta}{g \cos^2 \alpha} [\cos \beta \cdot \cos \alpha - \sin \alpha \cdot \sin \beta] \\\\ \implies & \quad L = \frac{2 \ v_0^2 \sin \beta}{g \cos^2 \alpha} \cos (\alpha + \beta) \end{align*}$
$(c)$ For range $(L)$ to be maximum, $ \sin \beta \cdot \cos (\alpha + \beta) $ should be maximum.
Let,
$ \begin{align*} Z &= \sin \beta \cdot \cos (\alpha + \beta) \\ &= \sin \beta \left[ \cos \alpha \cdot \cos \beta - \sin \alpha \cdot \sin \beta \right] \\ &= \frac{1}{2} \left[ \cos \alpha \cdot \sin 2\beta - 2 \sin \alpha \cdot \sin^2 \beta \right] \\ &= \frac{1}{2} \left[ \sin 2 \beta \cdot \cos \alpha - \sin \alpha \left(1 - \cos 2 \beta\right) \right] \\ \implies z &= \frac{1}{2} \left[ \sin 2 \beta \cdot \cos \alpha - \sin \alpha + \sin \alpha \cdot \cos 2 \beta \right] \\ &= \frac{1}{2} \left[ \sin 2 \beta \cdot \cos \alpha + \cos 2 \beta \cdot \sin \alpha - \sin \alpha \right] \\ &= \frac{1}{2} \left[ \sin (2 \beta + \alpha) - \sin \alpha \right] \end{align*} $
For $z$ to be maximum,
$ \sin (2 = \beta + \alpha) = \text{maximum} = 1 $
$ \implies 2 \beta + \alpha = \frac{\pi}{2} \text{ or, } \beta = \frac{\pi}{4} - \frac{\alpha}{2} $