Give examples of a one-dimensional motion where
(a) the particle moving along positive x-direction comes to rest periodically and moves forward.
(b) the particle moving along positive x-direction comes to rest periodically and moves backward.
When we are writing an equation belonging to periodic nature it will involve sine or cosine function.
(a) The particle will be moving along positive x-direction only if t > sin t
Hence,
x(t) = 1 - sin t
Velocity v(t) = $\frac{dx(t)}{dt}$
v(t) = 1 - cos t
Acceleration a(t) = $\frac{dv}{dt}$
a(t) = sin t
When t = 0; x(t) = 0
When t = $\pi$; x(t) = $\pi$ > 0
When t = 0; x(t) = 2$\pi$ > 0
(b) Equation can be represented by
x(t) = sin t
v = $\frac{d}{dt}$ x(t) = cos t
As displacement and velocity are involving sin t and cos t hence these equations represent periodic.
Give example of a motion where x > 0, v < 0, a > 0 at a particular instant.
Let the motion is represented by
x(t) = A + Be-$\gamma$t ... (i)
$$ \begin{aligned} &\text{Let} A >B \text { and } \gamma>0 \\\\ &\text{Now velocity} \,x(t) =\frac{d x}{d t}=-B \gamma e^{-\gamma t} \\\\ &\text{Acceleration} \, a(t) =\frac{d x}{d t}=B \gamma^2 e^{-\gamma t} \end{aligned} $$
Suppose we are considering any instant $t$, then from Eq. (i), we can say that
$x(t)>0 ; v(t)<0$ and $a>0$
An object falling through a fluid is observed to have acceleration given by $a = g - bv$ where $g$ = gravitational acceleration and $b$ is constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?
When speed becomes constant acceleration $a=\frac{d v}{d t}=0$
Given acceleration
$$ a=g-b v $$
where, $g=$ gravitational acceleration
Clearly, from above equation as speed increases acceleration will decrease. At a certain speed say $v_0$, acceleration will be zero and speed will remain constant.
Hence,
$$ \begin{aligned} &a =g-b v_0=0 \\\\ &v_0 =g / b \end{aligned} $$
A ball is dropped and its displacement versus time graph is as shown (Displacement $x$ from ground and all quantities are positive upwards).
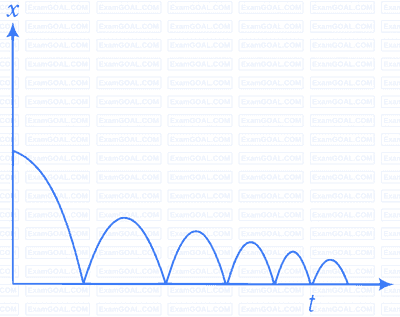
(a) Plot qualitatively velocity vs time graph
(b) Plot qualitatively acceleration vs time graph
It is clear from the graph that displacement $x$ is positive throughout. Ball is dropped from a height and its velocity increases in downward direction due to gravity pull. In this condition $v$ is negative but acceleration of the ball is equal to acceleration due to gravity i.e., $a=-g$. When ball rebounds in upward direction its velocity is positive but acceleration is $a=-g$.
(a) The velocity-time graph of the ball is shown in fig. (i).

(b) The acceleration-time graph of the ball is shown in fig. (ii).

A particle executes the motion described by $x(t) = x_{0}(1 - e^{-γt})$; $t \geq 0$, $x_{0} > 0$.
(a) Where does the particle start and with what velocity?
(b) Find maximum and minimum values of $x(t)$, $v(t)$, $a(t)$. Show that $x(t)$ and $a(t)$ increase with time and $v(t)$ decreases with time.
Given,
$x(t) = x_{0}(1 - e^{-γt})$
$v(t) = \dfrac{dx(t)}{dt} = x_{0}γe^{-γt}$
$a(t) = \dfrac{dv(t)}{dt} = - x_{0}γ^{2}e^{-γt}$
(a) When $t = 0$; $x(t) = x_{0}(1 - e^{0}) = x_{0}(1 - 1) = 0$
$x(t = 0) = x_{0}γe^{0} = x_{0}γ(1) = γx_{0}$
(b) $x(t)$ is maximum when $t = ∞$ $[x(t)]_{max} = x_{0}$
$x(t)$ is minimum when $t = 0$ $[x(t)]_{min} = 0$
$v(t)$ is maximum when $t = 0$; $v(0) = x_{0}γ$
$v(t)$ is minimum when $t = ∞$; $v(∞) = 0$
$a(t)$ is maximum when $t = ∞$; $a(∞) = 0$
$a(t)$ is minimum when $t = 0$; $a(0) = - x_{0}γ^{2}$
Note We should be careful about the nature of variation of the curve and maximum and minimum value will be decided accordingly.