During a total solar eclipse the moon almost entirely covers the sphere of the sun. Write the relation between the distances and sizes of the sun and moon.
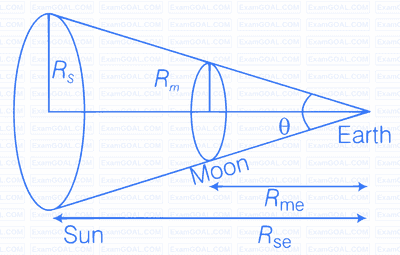
Consider the diagram given below
$R_{m e}=$ Distance of moon from earth
$R_{\text {se }}=$ Distance of sun from earth
Let angle made by sun and moon is $\theta$, we can write
$$ \theta=\frac{A_{\text {sun }}}{R_{\mathrm{se}}^2}=\frac{A_{\text {moon }}}{R_{\text {me }}^2} $$
$$ \text { Here, } \begin{aligned} A_{\text {sun }} & =\text { Area of the sun } \\\\ A_{\text {moon }} & =\text { Area of the moon } \end{aligned} $$
$$ \begin{array}{llrl} \Rightarrow & \theta =\frac{\pi R_s^2}{R_{s e}^2}=\frac{\pi R_m^2}{R_{m e}^2} \\\\ \Rightarrow & \left(\frac{R_s}{R_{s e}}\right)^2 =\left(\frac{R_m}{R_{m e}}\right)^2 \\\\ \Rightarrow & \frac{R_s}{R_{s e}} =\frac{R_m}{R_{m e}} \\\\ \Rightarrow & \frac{R_s}{R_m} =\frac{R_{s e}}{R_{m e}} \end{array} $$
$$ \text { (Here, radius of sun and moon represents their sizes respectively) } $$
If the unit of force is 100 N, unit of length is 10 m and the unit of time is 100 s, what is the unit of mass in this system of units?
Dimension of force $F = [MLT^{-2}] = 100 N $ ... (i)
Length $(L) = [L] = 10 m $ ... (ii)
Time $(t) = [T] = 100 s $ ... (iii)
Substituting values of $L$ and $T$ from Eqs. (ii) and (iii) in Eq. (i), we get
$\begin{aligned}& \Rightarrow \frac{M \times 10}{100 \times 100} =100 \\\\ & \Rightarrow M =100 \times 1000 \mathrm{~kg} \\\\ & M =10^5 \mathrm{~kg} \end{aligned}$
Give an example of:
(a) a physical quantity which has a unit but no dimensions
(b) a physical quantity which has neither unit nor dimensions
(c) a constant which has a unit
(d) a constant which has no unit
(a) Plane angle $ \theta = \frac{L}{r} \text{radian}$
its unit is radian but has no dimensions
(b) Strain $ = \frac{\Delta L}{L} = \frac{\text{Change in length}}{\text{length}}$
It has neither unit nor dimensions
(c) Gravitational constant (G) = $6.67 \times 10^{-11} \text{N} m^{2} / \text{kg}^{2}$
(d) Reynold’s number is a constant which has no unit.
Calculate the length of the arc of a circle of radius $31.0 \text{ cm}$ which subtends an angle of $ \frac{ \pi}{6}$ at the centre.
We know that angle $ \theta = \frac{l}{r} \text{radian}$
Given, $ \theta = \frac{ \pi}{6} = \frac{l}{31 \text{ cm}}$
Hence, length $l = 31 \times \frac{ \pi}{6} \text{ cm} = \frac{31 \times 3.14}{6} \text{ cm} = 16.22 \text{ cm}$
Rounding off to three significant figures it would be $16.2 \text{ cm}$.
Calculate the solid angle subtended by the periphery of an area of $1\text{cm}^{2}$ at a point situated symmetrically at a distance of $5 \text{ cm}$ from the area.
We know that solid angle $ \Omega = \frac{\text{Area}}{(\text{Distance})^{2}}$
$= \frac{1 \text{cm}^{2}}{(5 \text{cm})^{2}}= \frac{1}{25} = 4 \times 10^{-2} \text{ steradian}$
(∵ Area = $1 \text{cm}^{2}$, distance = $5 \text{ cm}$)
Note We should not confuse, solid angle with plane angle $ \theta = \frac{l}{r} \text{ radian}$.