Which of the following time measuring devices is most precise?
A wall clock
A stop watch
A digital watch
An atomic clock
A wall clock can measure time correctly upto one second. A stop watch can measure time correctly upto a fraction of a second. A digital watch can measure time upto a fraction of second. An atomic clock can measure time most precisely as its precision is 1s in 1013 s.
The distance of a galaxy is of the order of 1025 m. Calculate the order of magnitude of time taken by light to reach us from the galaxy.
Given, distance of the galaxy = 1025 m
Speed of light = 3 × 108 m/s
Hence, time taken by light to reach us from galaxy is,
$t = \frac{\text{Distance}}{\text{Speed}} = \frac{10^{25}}{3 \times 10^8} \approx \frac{1}{3} \times 10^{17} = \frac{10}{3} \times 10^{16} = 3.33 \times 10^{16}$ s
The vernier scale of a travelling microscope has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5 mm, calculate the minimum inaccuracy in the measurement of distance.
Note:
Inaccuracy will be measured by the difference of 1MSD and 1VSD, where MSD = main scale division and VSD = vernier scale division.
By question, it is given that:
$50VSD = 49MSD $
$1MSD = \frac{50}{49} VSD $
$1VSD = \frac{49}{50} MSD $
Minimum inaccuracy = $1MSD - 1VSD $
$= 1MSD - \frac{49}{50}MSD $
$= \frac{1}{50} MSD $
Given, $1MSD = 0.5 $ mm
Hence, minimum inaccuracy = $\frac{1}{50} \times 0.5 $ mm $= \frac{1}{100} $ mm = 0.01 mm
During a total solar eclipse the moon almost entirely covers the sphere of the sun. Write the relation between the distances and sizes of the sun and moon.
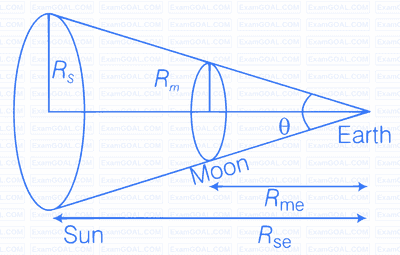
Consider the diagram given below
$R_{m e}=$ Distance of moon from earth
$R_{\text {se }}=$ Distance of sun from earth
Let angle made by sun and moon is $\theta$, we can write
$$ \theta=\frac{A_{\text {sun }}}{R_{\mathrm{se}}^2}=\frac{A_{\text {moon }}}{R_{\text {me }}^2} $$
$$ \text { Here, } \begin{aligned} A_{\text {sun }} & =\text { Area of the sun } \\\\ A_{\text {moon }} & =\text { Area of the moon } \end{aligned} $$
$$ \begin{array}{llrl} \Rightarrow & \theta =\frac{\pi R_s^2}{R_{s e}^2}=\frac{\pi R_m^2}{R_{m e}^2} \\\\ \Rightarrow & \left(\frac{R_s}{R_{s e}}\right)^2 =\left(\frac{R_m}{R_{m e}}\right)^2 \\\\ \Rightarrow & \frac{R_s}{R_{s e}} =\frac{R_m}{R_{m e}} \\\\ \Rightarrow & \frac{R_s}{R_m} =\frac{R_{s e}}{R_{m e}} \end{array} $$
$$ \text { (Here, radius of sun and moon represents their sizes respectively) } $$
If the unit of force is 100 N, unit of length is 10 m and the unit of time is 100 s, what is the unit of mass in this system of units?
Dimension of force $F = [MLT^{-2}] = 100 N $ ... (i)
Length $(L) = [L] = 10 m $ ... (ii)
Time $(t) = [T] = 100 s $ ... (iii)
Substituting values of $L$ and $T$ from Eqs. (ii) and (iii) in Eq. (i), we get
$\begin{aligned}& \Rightarrow \frac{M \times 10}{100 \times 100} =100 \\\\ & \Rightarrow M =100 \times 1000 \mathrm{~kg} \\\\ & M =10^5 \mathrm{~kg} \end{aligned}$