Give example of a motion where x > 0, v < 0, a > 0 at a particular instant.
Let the motion is represented by
x(t) = A + Be-$\gamma$t ... (i)
$$ \begin{aligned} &\text{Let} A >B \text { and } \gamma>0 \\\\ &\text{Now velocity} \,x(t) =\frac{d x}{d t}=-B \gamma e^{-\gamma t} \\\\ &\text{Acceleration} \, a(t) =\frac{d x}{d t}=B \gamma^2 e^{-\gamma t} \end{aligned} $$
Suppose we are considering any instant $t$, then from Eq. (i), we can say that
$x(t)>0 ; v(t)<0$ and $a>0$
An object falling through a fluid is observed to have acceleration given by $a = g - bv$ where $g$ = gravitational acceleration and $b$ is constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?
When speed becomes constant acceleration $a=\frac{d v}{d t}=0$
Given acceleration
$$ a=g-b v $$
where, $g=$ gravitational acceleration
Clearly, from above equation as speed increases acceleration will decrease. At a certain speed say $v_0$, acceleration will be zero and speed will remain constant.
Hence,
$$ \begin{aligned} &a =g-b v_0=0 \\\\ &v_0 =g / b \end{aligned} $$
A ball is dropped and its displacement versus time graph is as shown (Displacement $x$ from ground and all quantities are positive upwards).
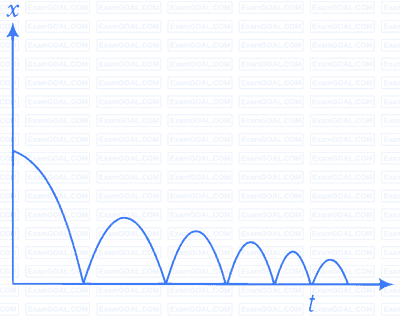
(a) Plot qualitatively velocity vs time graph
(b) Plot qualitatively acceleration vs time graph
It is clear from the graph that displacement $x$ is positive throughout. Ball is dropped from a height and its velocity increases in downward direction due to gravity pull. In this condition $v$ is negative but acceleration of the ball is equal to acceleration due to gravity i.e., $a=-g$. When ball rebounds in upward direction its velocity is positive but acceleration is $a=-g$.
(a) The velocity-time graph of the ball is shown in fig. (i).

(b) The acceleration-time graph of the ball is shown in fig. (ii).

A particle executes the motion described by $x(t) = x_{0}(1 - e^{-γt})$; $t \geq 0$, $x_{0} > 0$.
(a) Where does the particle start and with what velocity?
(b) Find maximum and minimum values of $x(t)$, $v(t)$, $a(t)$. Show that $x(t)$ and $a(t)$ increase with time and $v(t)$ decreases with time.
Given,
$x(t) = x_{0}(1 - e^{-γt})$
$v(t) = \dfrac{dx(t)}{dt} = x_{0}γe^{-γt}$
$a(t) = \dfrac{dv(t)}{dt} = - x_{0}γ^{2}e^{-γt}$
(a) When $t = 0$; $x(t) = x_{0}(1 - e^{0}) = x_{0}(1 - 1) = 0$
$x(t = 0) = x_{0}γe^{0} = x_{0}γ(1) = γx_{0}$
(b) $x(t)$ is maximum when $t = ∞$ $[x(t)]_{max} = x_{0}$
$x(t)$ is minimum when $t = 0$ $[x(t)]_{min} = 0$
$v(t)$ is maximum when $t = 0$; $v(0) = x_{0}γ$
$v(t)$ is minimum when $t = ∞$; $v(∞) = 0$
$a(t)$ is maximum when $t = ∞$; $a(∞) = 0$
$a(t)$ is minimum when $t = 0$; $a(0) = - x_{0}γ^{2}$
Note We should be careful about the nature of variation of the curve and maximum and minimum value will be decided accordingly.
A bird is tossing (flying to and fro) between two cars moving towards each other on a straight road. One car has a speed of 18 km/h while the other has the speed of 27 km/h. The bird starts moving from the first car towards the other and is moving with the speed of 36 km/h and when the two cars were separated by 36 km. What is the total distance covered by the bird?
To determine the total distance covered by the bird, let's proceed step-by-step.
First, we need to calculate the time it takes for the two cars to meet. The two cars are moving towards each other, so their relative speed is the sum of their individual speeds.
The speed of the first car is 18 km/h and the speed of the second car is 27 km/h. Therefore, their relative speed is:
$$18 \, \text{km/h} + 27 \, \text{km/h} = 45 \, \text{km/h}$$
The initial distance between the two cars is 36 km. To find the time it takes for the cars to meet, we use the formula:
$$\text{Time} = \frac{\text{Distance}}{\text{Relative Speed}}$$
Substituting the provided values, we get:
$$\text{Time} = \frac{36 \, \text{km}}{45 \, \text{km/h}} = \frac{4}{5} \, \text{hours} = 0.8 \, \text{hours}$$
Now, we know that the bird is flying at a speed of 36 km/h. To find the total distance covered by the bird while the two cars meet, we use the formula:
$$\text{Distance} = \text{Speed} \times \text{Time}$$
Substituting the speed of the bird and the time calculated, we get:
$$\text{Distance} = 36 \, \text{km/h} \times 0.8 \, \text{hours} = 28.8 \, \text{km}$$
Thus, the total distance covered by the bird is 28.8 kilometers.